Comment identifier la plus grande variation de performances dans Excel (en valeur absolue)

Dans ce tutoriel, je vais vous montrer comment identifier automatiquement quelle donnée a connu la plus grande variation entre deux périodes, que cette variation soit positive ou négative.

Nous allons découvrir ensemble plusieurs techniques allant de la plus simple à la plus avancée, incluant des formules matricielles et des fonctions peu connues d'Excel.

À la fin de ce tutoriel, vous saurez exactement quelle méthode choisir selon votre situation et votre niveau de maîtrise d'Excel.

Téléchargement

Vous pouvez télécharger le fichier d'exemple de cet article en cliquant sur le lien suivant :

Tutoriel Vidéo

1. Présentation

Pour illustrer ce tutoriel, nous allons pouvoir utiliser le tableau suivant dans lequel nous gérons les performances commerciales d'une équipe de six vendeurs.

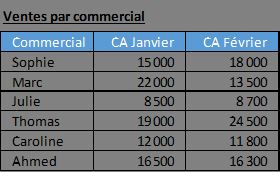
Ce tableau contient les chiffres d'affaires réalisés par chaque commercial sur deux mois consécutifs : janvier et février.

Notre objectif est donc de déterminer automatiquement quel commercial a connu la plus forte évolution de son chiffre d'affaires, qu'il s'agisse d'une amélioration importante ou d'une baisse significative.

Dans ce contexte, nous cherchons la variation en valeur absolue, ce qui signifie que nous voulons comparer les hausses et les baisses sur un pied d'égalité.

Si nous observons rapidement notre tableau, nous constatons que Sophie a progressé de 3000 euros, Marc a chuté de 8500 euros, Thomas a augmenté de 5500 euros.

La question qui se pose est donc : comment Excel peut-il nous indiquer automatiquement que Marc détient la plus grande variation avec 8500 euros, même si cette variation est négative ?

Cette problématique est très courante dans le monde professionnel. Nous pouvons l'appliquer à l'analyse de stocks de produits, à l'évolution des ventes de magasins, aux variations de températures, aux fluctuations boursières, ou à n'importe quelle comparaison de données entre deux périodes.

La maîtrise de ces techniques va donc nous faire gagner un temps considérable dans nos analyses quotidiennes.

2. La méthode classique avec colonne auxiliaire

   2.1. Création de la colonne de calcul

Commençons par la méthode la plus accessible, que tout utilisateur d'Excel peut mettre en place dès sa première utilisation du logiciel, qui consiste à ajouter une « colonne auxiliaire » dans laquelle nous allons effectuer nos calculs intermédiaires.

Nous nous positionnons dans la cellule D13 et nous saisissons l'en-tête « Variation ».

Ensuite, nous cliquons sur la cellule D8, juste en face du premier commercial, Sophie.

C'est ici que nous allons construire notre formule de calcul. Nous allons utiliser une fonction très importante d'Excel qui s'appelle ABS(), qui signifie « valeur absolue ».

Cette fonction mathématique transforme n'importe quel nombre négatif en nombre positif, tout en laissant les nombres positifs inchangés.

Nous saisissons donc la formule suivante dans la cellule D8 :

=ABS(C8-B8)

Nous calculons simplement la différence entre le chiffre d'affaires de février et celui de janvier, et nous encapsulons ce résultat en tant qu’argument de la fonction ABS(), afin de s’assurer que le résultat sera toujours positif.

Maintenant, nous devons appliquer cette formule aux cinq autres commerciaux en positionnant le curseur de la souris sur le petit carré noir qui se trouve en bas à droite de la cellule, que nous appelons la « poignée de recopie ». Puis, nous double-cliquons sur cette poignée pour permettre à Excel d’étendre la formule jusqu'à la dernière ligne contenant des données adjacentes.

   2.2. Identification du maximum

Maintenant que nous avons calculé toutes les variations en valeur absolue, nous devons identifier quelle est la plus grande.

Pour cela, nous allons utiliser la fonction MAX(), qui est l'une des fonctions les plus élémentaires d'Excel.

Nous nous positionnons dans une cellule vide, par exemple la cellule G8, où nous allons afficher notre résultat final. Nous saisissons la formule suivante :

=MAX(D8:D13)

Cette formule parcourt toute la plage D8:D13, c'est-à-dire toutes nos variations calculées précédemment, et nous retourne la valeur la plus élevée.

Dans notre cas, Excel affiche 8500, qui correspond effectivement à la variation de Marc.

Cette méthode présente plusieurs avantages, notamment celui d’être très visuelle : nous pouvons voir d'un coup d'œil toutes les variations calculées dans la colonne D, ce qui facilite la vérification et la compréhension.

Ensuite, elle fonctionne avec toutes les versions d'Excel, même les plus anciennes, ce qui garantit une compatibilité totale si nous devons partager notre fichier avec des collègues utilisant des versions différentes.

Cependant, cette méthode a un petit inconvénient esthétique : elle nécessite une colonne supplémentaire qui peut encombrer notre tableau, surtout si nous devons le présenter lors d'une réunion ou l'imprimer pour un rapport.

Nous pouvons donc la masquer tout en conservant son contenu et ses calculs actifs. Pour cela, nous cliquons avec le bouton droit de la souris sur l'en-tête de la colonne D, là où est écrit la lettre « D ». Un menu contextuel apparaît, et nous sélectionnons l'option « Masquer ».

La colonne D disparaît immédiatement de notre vue, mais attention : elle n'est pas supprimée. Toutes nos formules continuent de fonctionner normalement en arrière-plan. Notre formule en G8 affiche toujours le résultat correct de 8500, même si nous ne voyons plus la colonne D.

3. La formule matricielle unique

   3.1. Principe des formules matricielles

Passons maintenant à une approche plus avancée qui va nous permettre d'obtenir le même résultat sans utiliser de colonne auxiliaire. Cette technique fait appel à ce qu'on appelle une « formule matricielle », qui est une formule capable d'effectuer plusieurs calculs simultanés sur des plages entières de cellules.

Le concept des formules matricielles peut sembler abstrait au début, mais il est en réalité assez simple. Imaginez que nous voulions calculer mentalement la variation de chaque commercial, puis identifier le maximum. Notre cerveau effectue ces opérations étape par étape : nous calculons 18000 moins 15000, puis 13500 moins 22000, et ainsi de suite. Une formule matricielle fait exactement la même chose, mais en une seule instruction.

Dans Excel, lorsque nous écrivons une formule classique comme « =C8-B8 », Excel effectue un seul calcul et nous donne un seul résultat. Mais avec une formule matricielle, nous pouvons écrire « =C8:C13-B8:B13 », et Excel va comprendre qu'il doit effectuer six calculs différents : C8 moins B8, C3 moins B3, et ainsi de suite jusqu'à C13 moins B13.

Le défi est que certaines fonctions Excel, comme MAX(), ne savent pas naturellement comment traiter ces multiples résultats simultanés. Nous devons donc leur indiquer explicitement qu'il s'agit d'une formule matricielle, et c'est là qu'intervient une combinaison de touches spéciale que nous allons découvrir.

   3.2. Construction de la formule

Nous nous positionnons dans une cellule vide, par exemple la cellule F4, où nous allons construire notre formule matricielle. Nous commençons par taper la fonction MAX(), puis nous ouvrons la parenthèse. À l'intérieur, nous allons imbriquer la fonction ABS().

=MAX(ABS(C8:C13-B8:B13))

Nous demandons ici à Excel de calculer toutes les différences entre les chiffres d'affaires de février et ceux de janvier. Cela génère un tableau invisible de six valeurs : 3000, -8500, 200, 5500, -200, -200.

Ensuite, la fonction ABS() s'applique à chacune de ces six valeurs et les transforme en valeurs absolues : 3000, 8500, 200, 5500, 200, 200. Finalement, la fonction MAX() parcourt ces six résultats et nous retourne le plus grand, soit 8500.

Mais attention, et c'est ici que réside toute la particularité des formules matricielles : nous ne devons pas valider cette formule en appuyant simplement sur la touche [Entrée] comme nous le faisons habituellement.

Si nous faisions cela, Excel nous retournerait une erreur #VALEUR!, car il ne comprendrait pas qu'il doit traiter cette formule comme une opération matricielle.

À la place, après avoir tapé notre formule, nous devons appuyer simultanément sur les trois touches [Ctrl]+[Maj]+[Entrée].

Cette combinaison de touches signale à Excel : « Attention, cette formule doit être traitée comme une formule matricielle ».

Lorsque nous validons avec [Ctrl]+[Maj]+[Entrée], Excel ajoute automatiquement des accolades autour de notre formule, qui devient :

{=MAX(ABS(C8:C13-B8:B13))}

Ces accolades sont la signature visuelle d'une formule matricielle, mais attention, nous ne devons jamais taper ces accolades manuellement, c'est Excel qui les ajoute automatiquement quand nous validons avec [Ctrl]+[Maj]+[Entrée].

   3.3. Avantages et précautions

Cette méthode matricielle présente un avantage majeur : elle est élégante et compacte. Notre tableau reste propre, sans colonne supplémentaire, et pourtant nous obtenons le résultat recherché. Pour quelqu'un qui maîtrise bien Excel, cette formule est facile à lire et à comprendre d'un seul coup d'œil.

Cependant, elle comporte également un piège important à connaître. Si nous devons modifier cette formule ultérieurement, par exemple pour changer la plage de cellules ou ajuster un paramètre, nous devons absolument nous souvenir de valider à nouveau avec [Ctrl]+[Maj]+[Entrée].

Si nous validons par erreur avec la touche [Entrée] normale, Excel retire les accolades et la formule ne fonctionne plus correctement.

C'est pour cette raison que certains utilisateurs préfèrent éviter les formules matricielles dans les fichiers qu'ils partagent avec des collègues moins expérimentés.

Le risque qu'une personne modifie accidentellement la formule et oublie de valider avec [Ctrl]+[Maj]+[Entrée] est réel, et cela peut créer des erreurs difficiles à détecter dans des rapports importants.

4. Les techniques alternatives sans [Ctrl]+[Maj]+[Entrée]

   4.1. La fonction INDEX pour contourner les formules matricielles

Découvrons maintenant une méthode qui combine l'élégance de la formule unique, mais sans les contraintes des formules matricielles classiques.

Excel nous offre une astuce peu connue qui utilise la fonction INDEX() d'une manière inhabituelle pour contourner la nécessité d'appuyer sur [Ctrl]+[Maj]+[Entrée].

Nous nous positionnons dans la cellule F6 et nous saisissons la formule suivante :

=MAX(ABS(INDEX(C8:C13-B8:B13;0))) 

Cette fois-ci, nous pouvons valider normalement avec la touche [Entrée], sans utiliser [Ctrl]+[Maj]+[Entrée].

Pourtant, Excel va quand même effectuer correctement tous nos calculs et nous afficher 8500 comme résultat.

Le secret réside dans la fonction INDEX() et son deuxième argument, le zéro.

Normalement, INDEX() sert à extraire une valeur spécifique d'une plage de cellules en fonction de sa position.

Mais quand nous lui donnons 0 comme argument, nous forçons Excel à traiter l'ensemble de la plage comme un tableau complet, ce qui permet aux fonctions MAX() et ABS() de travailler correctement sur toutes les valeurs simultanément.

Cette technique est particulièrement appréciée dans les environnements professionnels où plusieurs personnes travaillent sur le même fichier. Elle élimine le risque d'oubli de la validation spéciale tout en conservant l'avantage d'une formule unique et compacte.

   4.2. La fonction AGREGAT pour plus de robustesse

Excel 2010 a introduit une fonction puissante appelée AGREGAT() qui peut naturellement traiter des opérations matricielles sans nécessiter la validation spéciale [Ctrl]+[Maj]+[Entrée].

Cette fonction est en quelque sorte un couteau suisse qui combine plusieurs fonctions statistiques en une seule, tout en offrant des options avancées de gestion des erreurs et des valeurs masquées.

Nous nous positionnons dans la cellule F8 et nous construisons la formule suivante :

=AGREGAT(14;4;ABS(C8:C13-B8:B13);1)

Où :

• Le premier argument, 14, est un code qui indique à Excel quelle opération statistique nous voulons effectuer. Le chiffre 14 correspond à la fonction GRANDE.VALEUR, qui est l'équivalent de MAX(). Excel utilise ces codes numérotés pour regrouper différentes fonctions : 1 pour MOYENNE, 4 pour MAX, 5 pour MIN, et ainsi de suite.
• Le deuxième argument, 4, spécifie comment AGREGAT() doit gérer les valeurs problématiques dans nos données. Le code 4 signifie « ignorer les valeurs d'erreur ». Cela rend notre formule beaucoup plus robuste : si l'une de nos cellules contient une erreur comme #DIV/0! ou #N/A, la formule continuera de fonctionner normalement au lieu de nous retourner une erreur.
• Le troisième argument est notre calcul habituel : ABS(C8:C13-B8:B13). Ici, AGREGAT() accepte naturellement cette expression matricielle sans aucun problème. Enfin, le dernier argument, 1, indique que nous voulons la première plus grande valeur, c'est-à-dire le maximum absolu.

Cette formule présente plusieurs avantages importants. Elle fonctionne avec une simple pression sur [Entrée], elle gère automatiquement les erreurs, et elle est même compatible avec les données filtrées : si nous appliquons un filtre sur notre tableau, AGREGAT() ne prendra en compte que les lignes visibles.

Le seul inconvénient de cette méthode est qu'elle nécessite Excel 2010 ou une version ultérieure. Si nous devons partager notre fichier avec quelqu'un qui utilise Excel 2007 ou une version antérieure, cette formule ne fonctionnera pas et affichera une erreur #NOM?.

5. Aller plus loin avec l'identification du commercial

Jusqu'à présent, nous avons appris à calculer la valeur de la plus grande variation, mais il se peut également que nous ayons besoin de savoir quel commercial ou quel produit est concerné par cette variation.

Nous allons donc ajouter une formule qui identifie automatiquement le nom du commercial correspondant.

Pour cela, nous allons utiliser une combinaison des fonctions INDEX() et EQUIV(). Nous nous positionnons dans la cellule G2 et nous saisissons :

=INDEX(A8:A13;EQUIV(G8;ABS(C8:C13-B8:B13);0)) 

La fonction EQUIV() cherche notre valeur maximale (qui se trouve en G8, soit 8500) dans la colonne des variations (D8:D13) et nous retourne sa position.

Dans notre cas, 8500 se trouve en deuxième position de la plage D8:D13. Ensuite, INDEX() prend cette position et va chercher le nom correspondant dans la colonne des commerciaux (A8:A13), ce qui nous donne « Marc ».

Cette technique fonctionne parfaitement sans qu’elles n’aie besoin d’être validée avec [Ctrl]+[Maj]+[Entrée] car elle ne contient pas d’expression matricielle.