Excel : testez 50 scénarios en 30 secondes (tutoriel complet)

Dans ce tutoriel, je vais vous montrer comment j'ai économisé des heures de travail la semaine dernière en utilisant une seule fonction Excel que 95% des utilisateurs ne connaissent pas.

Imaginez : vous avez un projet à lancer, vous devez tester 50 combinaisons différentes pour savoir si vous allez gagner ou perdre de l'argent.

Normalement, vous passeriez votre après-midi à modifier manuellement vos cellules, à recopier des valeurs, à faire des captures d'écran.

Mais si je vous dis qu'Excel peut faire tout ça en moins de 30 secondes avec une seule manipulation ?

C'est exactement ce que nous allons voir ensemble aujourd'hui avec les tableaux de données, une fonction cachée qui va littéralement transformer votre façon d'analyser vos projets.

Restez jusqu'à la fin car je vais aussi vous montrer comment identifier visuellement les meilleures options avec la mise en forme conditionnelle, une astuce que même certains formateurs Excel ignorent.

Téléchargement

Vous pouvez télécharger le fichier d'exemple de cet article en cliquant sur le lien suivant :

Tutoriel Vidéo

1. Présentation

Pour illustrer ce tutoriel, nous allons pouvoir utiliser le tableau suivant dans lequel nous gérons un projet de location de trottinettes électriques dans notre ville.

Ce tableau contient tous les paramètres financiers nécessaires pour évaluer la rentabilité de notre activité : les coûts fixes comme la location des trottinettes et l'assurance, les coûts variables comme la maintenance, ainsi que nos revenus attendus.

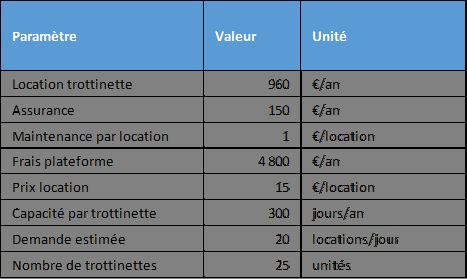
Ce tableau permet de voir clairement tous nos paramètres d'entrée au même endroit.

Nous remarquons que chaque ligne contient non seulement une valeur, mais aussi son unité de mesure (€/an, €/location, jours/an, etc.).

Cette précision est fondamentale car elle nous indique comment utiliser chaque valeur dans nos calculs.

Par exemple, si nous voyons « 960 €/an », nous savons immédiatement qu'il s'agit d'un coût annuel et que nous n'avons pas besoin de le multiplier par 12 comme nous le ferions pour un coût mensuel.

De plus, les cellules en jaune contiennent les variables que nous pourrons modifier plus tard : « Demande estimée » et « Nombre de trottinettes ».

Ce code couleur visuel nous permet d'identifier immédiatement quelles sont nos variables de décision, celles que nous pouvons ajuster pour tester différents scénarios.

2. Construction du modèle de base

Avant de commencer à construire nos formules, nous devons comprendre la logique du modèle.

Notre objectif est de déterminer le profit que nous pouvons réaliser en fonction de deux variables que nous ne contrôlons pas totalement : la demande quotidienne et le nombre de trottinettes que nous décidons de louer.

La difficulté vient du fait que nous devons signer un contrat de location annuel pour les trottinettes avant de connaître la demande réelle.

Nous prenons donc un risque : si nous louons trop de trottinettes et que la demande est faible, nous perdons de l'argent.

Si nous n'en louons pas assez et que la demande explose, nous ne pouvons pas satisfaire tous les clients.

Maintenant que les bases sont posées, nous allons nous intéresser à la section de calculs intermédiaires.

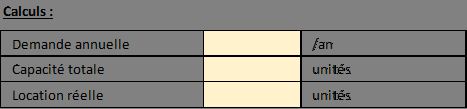
Ces calculs intermédiaires sont essentiels car ils vont transformer nos données quotidiennes en données annuelles, ce qui nous permet de tout calculer sur la même base temporelle.

Dans la cellule B20, nous calculons la demande annuelle avec la formule suivante :

=B20*365

Cette formule multiplie simplement notre demande quotidienne par 365 jours.

Pour une demande de 20 locations par jour, cela nous donne 7 300 locations par an.

Ensuite, nous calculons notre capacité totale, qui correspond au nombre maximum de locations que nous pouvons physiquement réaliser avec notre flotte de trottinettes :

=B14*B16

Cette formule multiplie le nombre de trottinettes par la capacité individuelle de chaque trottinette (300 jours/an).

Avec 25 trottinettes, nous obtenons une capacité totale de 7 500 locations par an.

Maintenant vient le calcul le plus important : les locations réelles.

En effet, nous ne pouvons pas louer plus de trottinettes que notre capacité physique, même si la demande est supérieure.

Nous devons donc prendre le minimum entre la demande et notre capacité :

=MIN(B20;B21)

La fonction MIN() compare les deux valeurs et retourne la plus petite.

Ce point est fondamental dans notre modèle : si la demande est de 10 000 locations mais que nous n'avons qu'une capacité de 7 500, nous ne pourrons réaliser que 7 500 locations.

C'est cette fonction qui va nous permettre de modéliser la contrainte de capacité de notre activité.

Passons maintenant à la section des coûts et revenus.

Le coût de location des trottinettes correspond au coût de location annuel (960 €) et l'assurance annuelle (150 €), puis nous multiplions par le nombre de trottinettes :

=(B9+B10)*B16

Ces frais de plateforme sont fixes :

=B12

Pour les coûts de maintenance, nous multiplions le coût unitaire par le nombre de locations réelles (et non la demande théorique) :

=B11*B22

Le total des coûts en cellule B21 additionne tous ces éléments :

=SOMME(B26:B28)

Ces revenus se calculent en multipliant le prix de location par les locations réelles :

=B13*B22

Enfin, le profit en cellule B23 est simplement la différence entre les revenus et les coûts :

=B22-B21

Notre modèle de base est maintenant opérationnel.

Si nous changeons la valeur de la demande en cellule B15 ou le nombre de trottinettes en cellule B16, tous les calculs se mettent automatiquement à jour.

3. Création du tableau de scénarios avec l'outil Tableau de données

Maintenant que notre modèle fonctionne, nous allons créer un tableau qui va calculer automatiquement le profit pour toutes les combinaisons possibles de demande et de nombre de trottinettes.

C'est là que la vraie puissance d'Excel entre en jeu.

Pour cela, nous allons construire un tableau avec les demandes en ligne et les nombres de trottinettes en colonne :

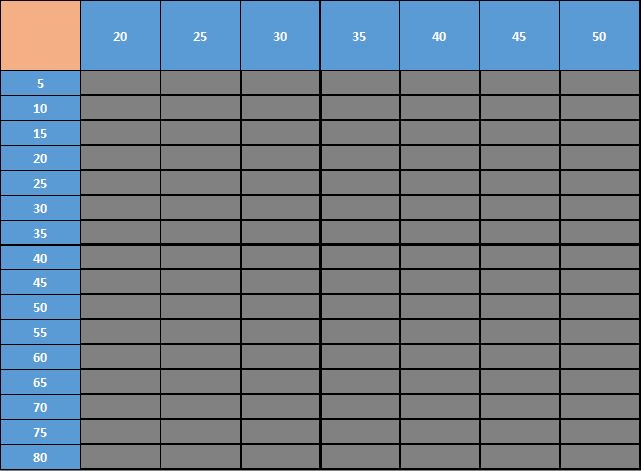
L'élément clé se trouve dans la cellule E8, à l'intersection de nos deux séries de valeurs.

C'est ici que nous devons placer une référence à notre cellule de profit :

=B31

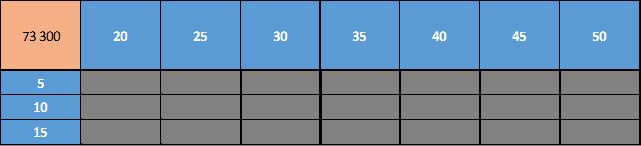
Cette cellule affiche maintenant le profit actuel de notre modèle.

C'est à partir de cette référence qu'Excel va calculer tous les autres scénarios.

Maintenant vient la magie.

Nous sélectionnons tout notre tableau, de E8 jusqu'à L24 : il est important de bien inclure la cellule avec la formule de profit, la ligne des demandes, la colonne des nombres de trottinettes et toutes les cellules vides au milieu.

Nous nous rendons dans l'onglet « Données », puis nous cliquons sur « Analyse de scénarios » et nous sélectionnons « Table de données ».

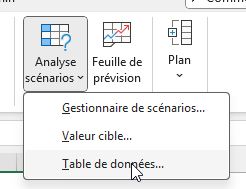
Une boîte de dialogue s'ouvre avec deux champs à renseigner.

Le champ « Cellule d'entrée en ligne » correspond à la cellule qui contient la variable des en-têtes de colonnes (le nombre de trottinettes, cellule B16) et le champ « Cellule d'entrée en colonne » correspond à la cellule qui contient la variable des en-têtes de lignes (la demande, en B16) :

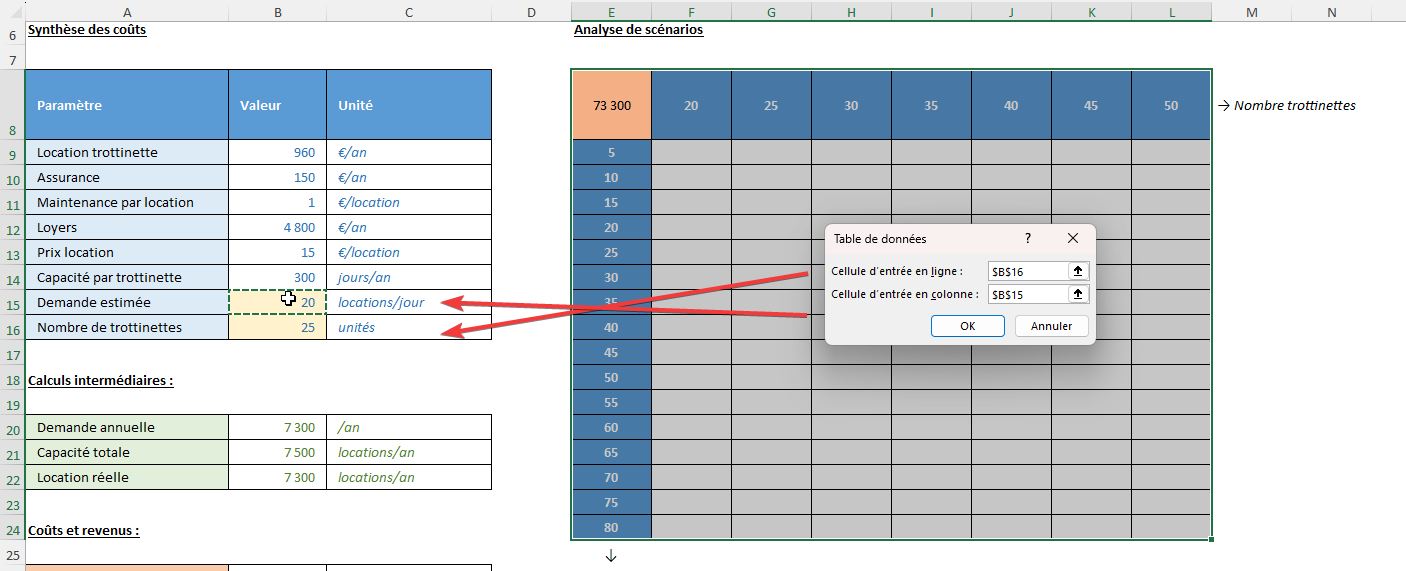
Nous appuyons sur le bouton « OK » et instantanément, Excel remplit tout le tableau avec les profits correspondant à chaque combinaison.

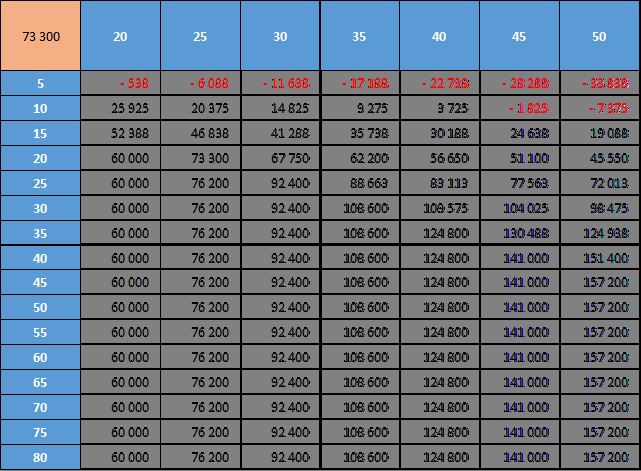
Nous pouvons maintenant voir que si nous avons 20 trottinettes et une demande de 5 locations par jour, nous réalisons une perte de -538€.

Nous retrouvons également le profit que nous avions calculé de 73 300€ correspondant à une demande 20 locations par jour pour un parc de 25 unités.

Une chose importante à comprendre : les cellules du tableau de données contiennent maintenant une formule spéciale qui commence par « {=TABLE(B16;B15)} » :

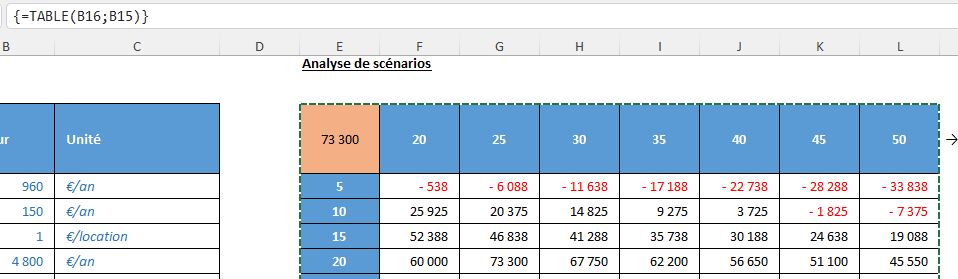
Les accolades indiquent qu'il s'agit d'une formule matricielle.

Nous ne devons jamais essayer de modifier une seule cellule du tableau, car cela casserait la formule.

Si nous voulons recalculer le tableau, nous devons sélectionner toute la plage et refaire l'opération complète.

4. Identification visuelle des meilleures options avec la mise en forme conditionnelle

Notre tableau contient maintenant beaucoup d'informations, mais il est difficile de repérer rapidement les meilleures options.

Nous allons utiliser la mise en forme conditionnelle pour faire ressortir visuellement les profits optimaux pour chaque niveau de demande.

Nous allons donc sélectionner les valeurs de ce tableau (cellule F9 à L24), puis nous nous rendons dans l'onglet « Accueil », nous cliquons sur « Mise en forme conditionnelle », puis « Nuances de couleurs », et enfin « Échelle de couleur Vert – Jaune - Rouge » :

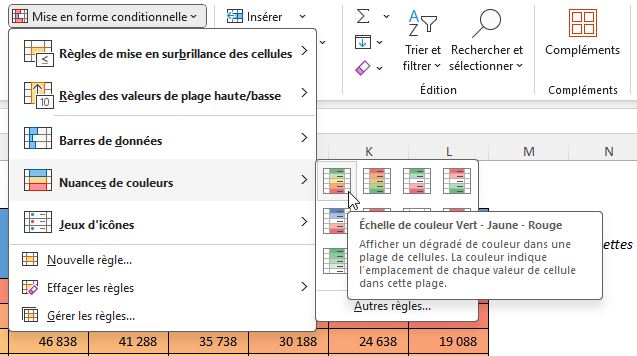
Nous avons maintenant une carte de chaleur qui va du rouge (pertes les plus importantes), vers le vert (profits les plus importants).

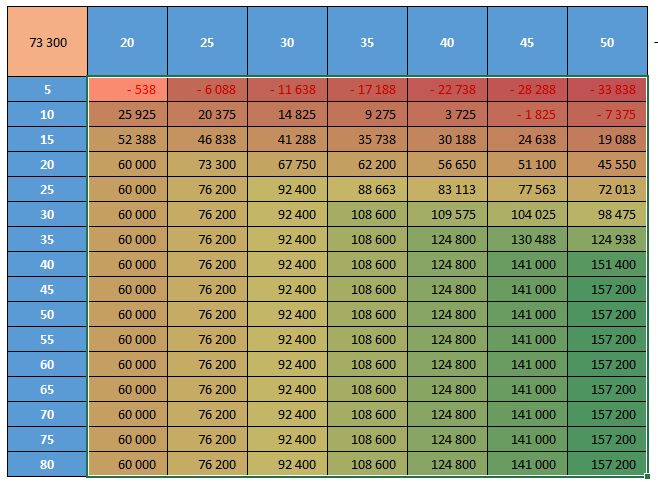
Notre tableau est maintenant parfaitement lisible : les meilleures options sont en vert, les pertes en rouge, et nous pouvons rapidement identifier les décisions optimales.

Par exemple, nous voyons clairement que pour une demande de 25 locations par jour, le meilleur profit (92 400 €) est obtenu avec 30 trottinettes, tandis que 35 trottinettes donnent un profit légèrement inférieur (88 663 €).

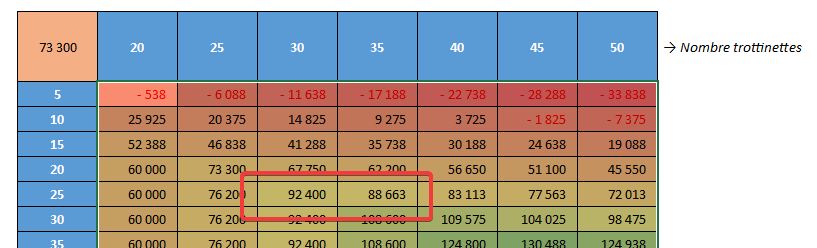
Cette différence montre que l'ajout de 5 trottinettes supplémentaires coûte plus cher en location et assurance qu'il ne rapporte en revenus additionnels à ce niveau de demande.